Kirchhoff’s Voltage-law, Current-law, Thevenin’s Theorem

Kirchhoff’s voltage law (KVL) and Kirchhoff’s Current law (KCL) are used to analyze Direct current circuits. The polarity of the voltage across resistances is significant in circuit analysis. The current direction is another factor that may be needed in circuit analysis. Electron flow will be used in this discussion. The negative end of the voltage across a resistor is where current enters.

Kirchhoff’s Voltage Law states that in an enclosed loop, taking into account polarity, the algebraic sum of all the voltages is equal to zero.

Kirchhoff’s Current law states that the sum of all currents flowing into a point equals the current leaving that point.

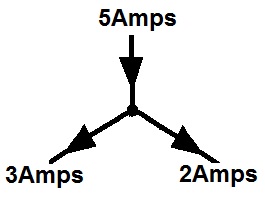
Superposition Theorem —The total current in any part of a linear circuit equals the algebraic sum of the currents produced by each source separately.

 Techniques such as the Superposition Theorem can be used to solve complex resistor current in the event that there is more than one voltage or current source.

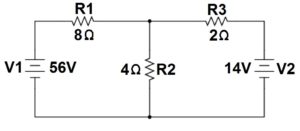
Example with two voltage sources

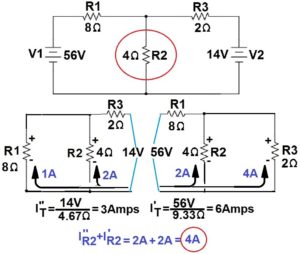
1. Choose one source.

2. Short all other voltage sources

3. Open all other current sources

4. Simplify the circuit by combining parallel and series networks

5. Calculate the current through simplified circuit

6. Work backward reestablishing parallel and series networks calculating resistor currents as you go(Direction of current must be noted)

7. Return to step one choosing a different source each time until all source values are calculated

8. Combine algebraically the currents through the complex resistor using the Superposition rule

9. Power can then be calculated using P= I²R

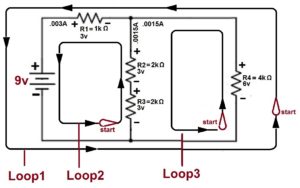
Mesh Current Analysis, uses simultaneous equations, Kirchhoff’s Voltage Law, and Ohms Law to determine unknown currents in a network. The example will show this method.

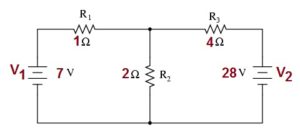
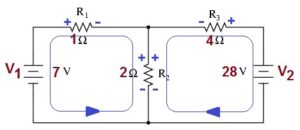
Example of solving R2 quantities using Mesh Current Analysis

Step 1. Identify all current loops within the circuit.

Step 2. Write Loop equations for each loop showing polarity and the IR value for each voltage in the loop

Step 3. Combine like terms for each loop equation and reduce them to their common denominator.

Step 4. Multiply one or both equations to obtain an opposite but equal factor

Step 5. Combine the two loop equations to factor one of the unknowns

Step 6. Reduce the remaining equation to obtain the value of the remaining factor

Step 7. Substitute that factor’s value back into one of the original loop equations to obtain the second unknown’s value. 

Thevenin’s Theorem will be discussed in the following post

Return to Electronics Post List